Numbers and symbols sometimes feel like a secret language, don't they? It's almost as if they hold important messages, but you need a special decoder ring to figure them out. Whether it's something as straightforward as adding things together or a bit more involved, these mathematical expressions are everywhere, helping us make sense of the world around us.
You see, in many situations, we come across problems where a piece of the puzzle is missing. Perhaps you're trying to figure out how many items you need, or maybe you're calculating a distance. This is where a little letter like 'x' comes into play, acting as a stand-in for that unknown value, just a little placeholder for whatever it is we're trying to discover. It's a way to represent something we don't quite know yet, but which we are eager to find out.
The phrase "x x x x is equal to" might look a bit unusual at first glance, but it's really just a friendly way of talking about how we figure out what that missing piece, that 'x', truly represents. It's about finding balance, about making sure one side of a mathematical statement matches the other. We often use tools and simple steps to reach a clear answer, basically making sense of these numerical puzzles. So, let's explore what this idea means and how we can get to the bottom of it.
- Chennai Express Download Filmyzilla Filmywap
- Filmywap Mp4moviez Filmyzilla In Hindi
- Filmyzilla Marathi Movie 2025
- Avatar Full Movie In Hindi Download Filmyzilla 720p
- Criminal Justice Web Series Filmyzilla
Table of Contents
- What Does 'x x x x is equal to' Really Mean?
- How a Simple Placeholder Works When x x x x is equal to Something
- Getting Help to Figure Out What x x x x is equal to
- When x x x x is equal to Itself - The Idea of x^3
- Are There Different Kinds of Answers When x x x x is equal to a Number?
- What Happens When x x x x is equal to 2?
- How Do We Figure Out What x x x x is equal to?
- Balancing the Sides When x x x x is equal to Something Else
What Does 'x x x x is equal to' Really Mean?
When you see "x x x x is equal to" in a problem, it's a way of asking you to find a particular value. Think of it like this: you have a statement, and on one side of an 'equals' sign, there's some kind of calculation or expression involving 'x', and on the other side, there's usually a number or another expression. The whole point is to figure out what 'x' has to be so that both sides of that 'equals' sign are perfectly matched. It's really about finding that sweet spot where everything balances out. For example, if you have something like "x + 5 = 10", you're looking for the number that, when you add five to it, gives you ten. It's a bit like a treasure hunt, actually.
How a Simple Placeholder Works When x x x x is equal to Something
The letter 'x' in these situations is just a stand-in. It's a symbol we use when we don't know the exact number yet, but we know it's there. So, when you see "x x x x is equal to", it's not some strange multiplication of 'x' four times, but rather a way of saying "what does 'x' need to be for this statement to hold true?" It's a very common way to represent an unknown quantity in all sorts of problems. In a way, it makes the problem easier to write down and think about, rather than saying "what number, when you do this and that to it, gives you this other number?" We use 'x' as a kind of shorthand, which is quite helpful.
Getting Help to Figure Out What x x x x is equal to
Sometimes, figuring out what 'x' stands for can feel a bit tricky, especially if the problem looks a little complicated. The good news is that there are many helpful tools out there designed to assist with this very thing. You can use an equation calculator, for instance, which lets you put in your problem and then it works through the steps to show you the answer. These tools are pretty clever, more or less, and can handle everything from very straightforward questions to ones that involve several steps. They're like having a little assistant who knows all the tricks to solve these kinds of puzzles, which is really quite handy.
- Hollywood Sci Fi Movies In Hindi Dubbed Download Filmywap Filmyzilla
- Flight Attendant Web Series Download Filmyzilla 720p
- Filyzilla
- Hindi Web Series Download Website List
- Hollywood Web Series In Hindi Dubbed
When x x x x is equal to Itself - The Idea of x^3
One common way you might see 'x' appear multiple times is when it's multiplied by itself. For example, if you see "x times x times x," which is written as "x*x*x", that's a special way of saying 'x' multiplied by itself three times. This is often represented in a shorter form as "x^3", where the small '3' tells you how many times 'x' is used in the multiplication. So, when "x x x x is equal to" refers to something like "x*x*x", it's asking you to find a number that, when multiplied by itself three separate times, reaches a specific total. This idea of 'cubing' a number comes up in many places, which is very interesting.
Are There Different Kinds of Answers When x x x x is equal to a Number?
When you're trying to find out what 'x' is equal to, the answer isn't always a neat, whole number that you can easily write down. Sometimes, the solution might be what we call an 'irrational' number. This means it's a number that goes on and on after the decimal point without any repeating pattern, so you can't express it perfectly as a simple fraction. It's a bit like trying to perfectly draw a circle; you can get very, very close, but there's always a little more to it. This happens when you're looking for things like the cube root of a number, which is pretty common when "x x x x is equal to" something like two.
What Happens When x x x x is equal to 2?
Take the problem where "x*x*x is equal to 2". The solution to this particular question is a number called the cube root of 2, often written with a special symbol that looks like a checkmark with a small '3' in it. This number is not something you can write as a simple fraction or a terminating decimal. It's an irrational number, meaning its decimal representation goes on endlessly without repeating. This specific problem also touches on a really fascinating part of mathematics where real numbers and what we call 'imaginary' numbers can sometimes blend, which is quite a complex idea but shows just how varied answers can be when "x x x x is equal to" certain values.
How Do We Figure Out What x x x x is equal to?
Solving for 'x' often involves a series of steps where you perform operations to both sides of the 'equals' sign to keep everything balanced. Imagine a seesaw: whatever you do to one side, you must do to the other to keep it level. For instance, if you have an equation like "2x + 3 = 7", the goal is to get 'x' all by itself on one side. You might start by taking away the same amount from both sides, then perhaps dividing both sides by a certain number. This way, you slowly but surely isolate 'x' until you find its true value. It's a bit like peeling an onion, layer by layer, until you get to the core, which is really quite satisfying.
Balancing the Sides When x x x x is equal to Something Else
The principle of keeping both sides balanced is absolutely key when "x x x x is equal to" a value. Every operation you apply, whether it's adding, subtracting, multiplying, or dividing, must be done equally to both sides of the equation. This ensures that the statement remains true and that you're always moving closer to finding the correct value for 'x'. This method is used in countless fields, from figuring out how much material you need in engineering to calculating forces in physics, or even understanding economic models. It's a very fundamental concept that helps us solve all sorts of practical problems, which is pretty neat.
Beyond Simple Numbers - Where Else Do We See x x x x is equal to?
The concept of 'x' and finding what it's equal to stretches far beyond just simple numbers. It shows up in more advanced areas of mathematics, like when you're working with functions, which are like rules that take an input and give you an output. For example, you might have a function where 'p(x) = x + 3', and then you're asked to figure out what 'p(x) + p(-x)' is equal to. This means you'd put 'x' into the rule, and then '-x' into the rule, and then add the results. It's a way of exploring how these rules behave and how they relate to each other, which is quite a bit more involved than just finding a single number.
Everyday Places Where x x x x is equal to a Value Matters
You might not always see the exact phrase "x x x x is equal to" in your daily life, but the underlying idea of finding an unknown value is constantly at play. From balancing your budget to planning a trip and calculating how much fuel you'll need, or even in more complex areas like designing new technologies, the core principle of solving for an unknown quantity is present. Experts in fields like chemistry, engineering, and economics rely on these ideas all the time to make predictions and solve problems. It's basically a fundamental tool for making sense of the world and making informed decisions, which is very useful.
What About Dividing x by x When x x x x is equal to a Fraction?
Sometimes, the unknown 'x' appears in a division problem, like "x divided by x". You might think that any number divided by itself is always one, and for most numbers, that's absolutely true. If you have 5 apples and you divide them among 5 people, everyone gets one apple. However, there's a special case when 'x' is zero. You see, dividing by zero is something we generally avoid in mathematics because it leads to an undefined situation. It's a bit like trying to share something among zero people; it just doesn't make logical sense. So, while "x divided by x is equal to 1" holds for almost every number, it does not apply when 'x' itself is zero, which is pretty important to remember.
When x is Zero and x x x x is equal to a Division Problem
When 'x' is zero, and you have an expression like 'x divided by x', it becomes a bit of a puzzle. While the direct answer is undefined, meaning we can't give it a specific numerical value, we can sometimes talk about what happens as 'x' gets incredibly close to zero. This idea is called a 'limit' in mathematics. For example, with an expression like "sin(x) divided by x", as 'x' gets closer and closer to zero, the value of the whole expression gets closer and closer to one, even though it's still technically undefined right at zero. This shows that even when "x x x x is equal to" a situation that seems impossible, there are often deeper mathematical ideas to explore.
Putting It All Together - The Idea of x x x x is equal to
From simple additions to complex equations involving powers and divisions, the idea of "x x x x is equal to" really boils down to finding a missing piece of information. It's about using logical steps and mathematical rules to balance an equation and reveal the hidden value of 'x'. Whether it's 'x' multiplied by itself three times, or 'x' in a simple addition problem, the goal is always to make sense of the relationship between different quantities. This fundamental concept is a cornerstone of how we solve problems and understand the numerical aspects of our world.
Related Resources:
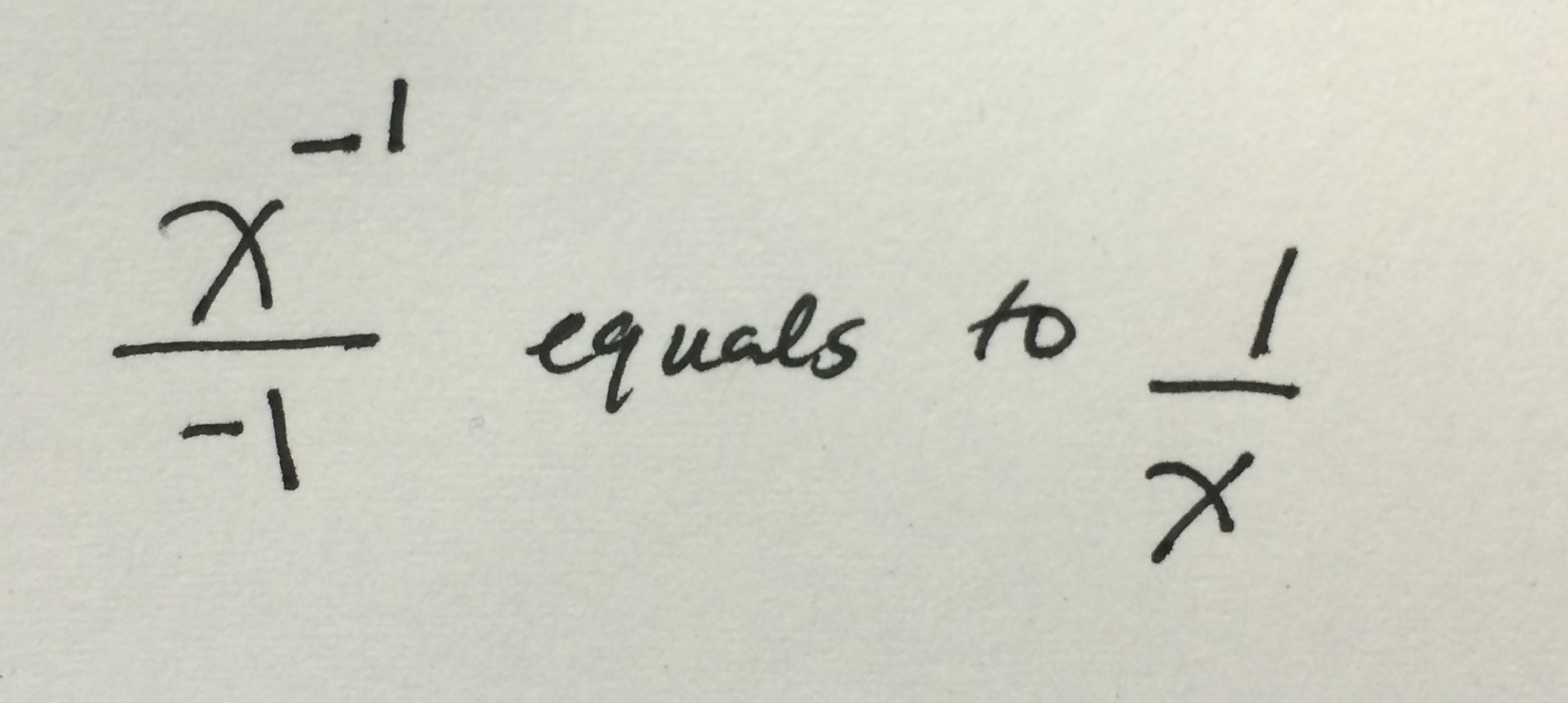
Detail Author:
- Name : Mason Heidenreich
- Username : taurean.okon
- Email : ruecker.favian@von.com
- Birthdate : 1970-09-25
- Address : 84815 Jaida Drive Carletonton, TX 98749
- Phone : 808-523-1026
- Company : Reichel-Pacocha
- Job : Environmental Science Technician
- Bio : Magnam exercitationem eligendi earum. Doloremque dolores vel unde sed. Est perferendis quis quibusdam harum similique. Voluptate libero quia amet quaerat dolore delectus omnis.
Socials
tiktok:
- url : https://tiktok.com/@mayertb
- username : mayertb
- bio : Consequuntur vel velit et aliquid illum sit placeat.
- followers : 1171
- following : 2873
twitter:
- url : https://twitter.com/bailey_mayert
- username : bailey_mayert
- bio : Veniam et modi sapiente. Earum doloremque voluptatem commodi rerum autem iure. Voluptatem molestiae voluptatum temporibus est id qui ipsam.
- followers : 359
- following : 687
linkedin:
- url : https://linkedin.com/in/bailey1503
- username : bailey1503
- bio : Non voluptas modi autem quis.
- followers : 5943
- following : 2450
facebook:
- url : https://facebook.com/bailey.mayert
- username : bailey.mayert
- bio : Nam reprehenderit optio perspiciatis odit dolorum dolores vero.
- followers : 1601
- following : 1885